Maximum flow problem
In optimization theory, the maximum flow problem is to find a feasible flow through a single-source, single-sink flow network that is maximum.
The maximum flow problem can be seen as a special case of more complex network flow problems, such as the circulation problem. The maximum value of an s-t flow is equal to the minimum capacity of an s-t cut in the network, as stated in the max-flow min-cut theorem.
Contents |
History
The maximum flow problem was first formulated in 1954 by T. E. Harris as a simplified model of Soviet railway traffic flow.[1] In 1955, Lester R. Ford and Delbert R. Fulkerson created the first known algorithm, the Ford–Fulkerson algorithm.[2][3]
Over the years, various improved solutions to the maximum flow problem were discovered, notably the shortest augmenting path algorithm of Edmonds and Karp and independently Dinitz; the blocking flow algorithm of Dinitz; the push-relabel algorithm of Goldberg and Tarjan; and the binary blocking flow algorithm of Goldberg and Rao. The electrical flow algorithm of Christiano, Kelner, Madry, and Spielman finds an approximately optimal maximum flow but only works in undirected graphs.
Definition
Let 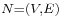 be a network with
be a network with 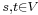 being the source and the sink of
being the source and the sink of 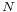 respectively.
respectively.
- The capacity of an edge is a mapping
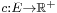 , denoted by
, denoted by 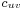 or
or 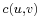 . It represents the maximum amount of flow that can pass through an edge.
. It represents the maximum amount of flow that can pass through an edge.
- A flow is a mapping
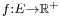 , denoted by
, denoted by 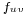 or
or 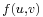 , subject to the following two constraints:
, subject to the following two constraints:
- 1.
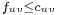 , for each
, for each 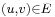 (capacity constraint: the flow of an edge cannot exceed its capacity)
(capacity constraint: the flow of an edge cannot exceed its capacity) - 2.
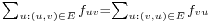 , for each
, for each 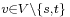 (conservation of flows: the sum of the flows entering a node must equal the sum of the flows exiting a node, except for the source and the sink nodes)
(conservation of flows: the sum of the flows entering a node must equal the sum of the flows exiting a node, except for the source and the sink nodes)
- 1.
- The value of flow is defined by
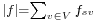 , where
, where 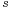 is the source of
is the source of 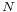 . It represents the amount of flow passing from the source to the sink.
. It represents the amount of flow passing from the source to the sink.
The maximum flow problem is to maximize 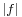 , that is, to route as much flow as possible from
, that is, to route as much flow as possible from 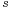 to
to 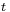 .
.
Solutions
We can define the Residual Graph, which provides a systematic way to search for forward-backward operations in order to find the maximum flow.
Given a flow network 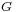 , and a flow
, and a flow 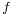 on
on 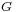 , we define the residual graph
, we define the residual graph 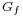 of
of 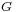 with respect to
with respect to 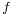 as follows.
as follows.
1. The node set of 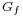 is the same as that of
is the same as that of 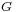 .
.
2. Each edge 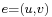 of
of 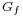 is with a capacity of
is with a capacity of 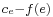 .
.
3. Each edge 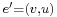 of
of 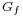 is with a capacity of
is with a capacity of 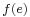 .
.
The following table lists algorithms for solving the maximum flow problem.
| Method | Complexity | Description |
|---|---|---|
| Linear programming | Constraints given by the definition of a legal flow. See the linear program here. | |
| Ford–Fulkerson algorithm | O(E max| f |) | As long as there is an open path through the residual graph, send the minimum of the residual capacities on the path.
The algorithm works only if all weights are integers. Otherwise it is possible that the Ford–Fulkerson algorithm will not converge to the maximum value. |
| Edmonds–Karp algorithm | O(VE2) | A specialization of Ford–Fulkerson, finding augmenting paths with breadth-first search. |
| Dinitz blocking flow algorithm | O(V2E) | In each phase the algorithms builds a layered graph with breadth-first search on the residual graph. The maximum flow in a layered graph can be calculated in O(VE) time, and the maximum number of the phases is n-1. In networks with unit capacities, Dinic's algorithm terminates in 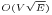 time. time. |
| General push-relabel maximum flow algorithm | O(V2E) | The push relabel algorithm maintains a preflow, i.e. a flow function with the possibility of excess in the vertices. The algorithm runs while there is a vertex with positive excess, i.e. an active vertex in the graph. The push operation increases the flow on a residual edge, and a height function on the vertices controls which residual edges can be pushed. The height function is changed with a relabel operation. The proper definitions of these operations guarantee that the resulting flow function is a maximum flow. |
| Push-relabel algorithm with FIFO vertex selection rule | O(V3) | Push-relabel algorithm variant which always selects the most recently active vertex, and performs push operations until the excess is positive or there are admissible residual edges from this vertex. |
| Dinitz blocking flow algorithm with dynamic trees | O(VE log(V)) | The dynamic trees data structure speeds up the maximum flow computation in the layered graph to O(Elog(V)). |
| Push-relabel algorithm with dynamic trees | O(VE log(V2/E)) | The algorithm builds limited size trees on the residual graph regarding to height function. These trees provide multilevel push operations. |
| Binary blocking flow algorithm [1] | 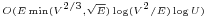 |
The value U corresponds to the maximum capacity of the network. |
| MPM (Malhotra, Pramodh-Kumar and Maheshwari) algorithm | O(V3) |
For a more extensive list, see [2].
Integral flow theorem
The integral flow theorem states that
- If each edge in a flow network has integral capacity, then there exists an integral maximal flow.
Application
Multi-source multi-sink maximum flow problem
Given a network N = (V,E) with a set of sources S = {s1, ..., sn} and a set of sinks T = {t1, ..., tm} instead of only one source and one sink, we are to find the maximum flow across N. We can transform the multi-source multi-sink problem into a maximum flow problem by adding a consolidated source connecting to each vertex in S and a consolidated sink connected by each vertex in T with infinite capacity on each edge (See Fig. 4.1.1.).
Minimum path cover in directed acyclic graph
Given a directed acyclic graph G = (V, E), we are to find the minimum number of paths to cover each vertex in V. We can construct a bipartite graph G' = (Vout∪Vin, E' ) from G, where
- Vout = {v∈V: v has positive out-degree}.
- Vin = {v∈V: v has positive in-degree}.
- E' = {(u,v)∈(Vout,Vin): (u,v)∈E}.
Then it can be shown that G' has a matching of size m if and only if there exists n-m paths that cover each vertex in G, where n is the number of vertices in G. Therefore, the problem can be solved by finding the maximum cardinality matching in G' instead.
Maximum cardinality bipartite matching
Given a bipartite graph G = (X∪Y, E), we are to find a maximum cardinality matching in G, that is a matching that contains the largest possible number of edges. This problem can be transformed into a maximum flow problem by constructing a network N = (X∪Y∪{s,t}, E' }, where
- E' contains the edges in G directed from X to Y.
- (s,x)∈E' for each x∈X and (y,t)∈E' for each y∈Y.
- c(e) = 1 for each e∈E' (See Fig. 4.3.1).
Then the value of the maximum flow in N is equal to the size of the maximum matching in G.
Maximum flow problem with vertex capacities
Given a network N = (V, E), in which there is capacity at each node in addition to edge capacity, that is, a mapping c: V→R+, denoted by c(v), such that the flow f has to satisfy not only the capacity constraint and the conservation of flows, but also the vertex capacity constraint
- Σi∈Vfiv ≤ c(v) for each v∈V∖{s,t}.
In other words, the amount of flow passing through a vertex cannot exceed its capacity.
To find the maximum flow across N, we can transform the problem into the maximum flow problem in the original sense by expanding N. First, each v∈V is replaced by vin and vout, where vin is connected by edges going into v and vout is connected to edges coming out from v, then assign capacity c(v) to the edge connecting vin and vout (See Fig. 4.4.1). In this expanded network, the vertex capacity constraint is removed and therefore the problem can be treated as the original maximum flow problem.
Maximum independent path
Given a directed graph G = (V, E) and two vertices s and t, we are to find the maximum number of independent paths from s to t. Two paths are said to be independent if they do not have a vertex in common apart from s and t. We can construct a network N = (V, E) from G with vertex capacities, where
- s and t are the source and the sink of N respectively.
- c(v) = 1 for each v∈V.
- c(e) = 1 for each e∈E.
Then the value of the maximum flow is equal to the maximum number of independent paths from s to t.
Maximum edge-disjoint path
Given a directed graph G = (V, E) and two vertices s and t, we are to find the maximum number of edge-disjoint paths from s to t. This problem can be transformed to a maximum flow problem by constructing a network N = (V, E) from G with s and t being the source and the sink of N respectively and assign each edge with unit capacity.
See also
References
- ^ Schrijver, Alexander, "On the history of the transportation and maximum flow problems", Mathematical Programming 91 (2002) 437-445
- ^ Ford, L.R., Jr.; Fulkerson, D.R., "Maximal Flow through a Network", Canadian Journal of Mathematics (1956), pp.399-404.
- ^ Ford, L.R., Jr.; Fulkerson, D.R., Flows in Networks, Princeton University Press (1962).
Notes
- ^ Andrew V. Goldberg and S. Rao (1998). "Beyond the flow decomposition barrier". J. Assoc. Comput. Mach. 45 (5): 753–782. doi:10.1145/290179.290181.
- ^ Andrew V. Goldberg and Robert E. Tarjan (1988). "A new approach to the maximum-flow problem". Journal of the ACM (ACM Press) 35 (4): 921–940. doi:10.1145/48014.61051. ISSN 0004-5411.
- ^ Joseph Cheriyan and Kurt Mehlhorn (1999). "An analysis of the highest-level selection rule in the preflow-push max-flow algorithm". Information Processing Letters 69 (5): 239–242. doi:10.1016/S0020-0190(99)00019-8.
- ^ Daniel D. Sleator and Robert E. Tarjan (1983). "A data structure for dynamic trees". Journal of Computer and System Sciences 26 (3): 362–391. doi:10.1016/0022-0000(83)90006-5. ISSN 0022-0000. http://www.cs.cmu.edu/~sleator/papers/dynamic-trees.pdf.
- ^ Daniel D. Sleator and Robert E. Tarjan (1985). "Self-adjusting binary search trees". Journal of the ACM (ACM Press) 32 (3): 652–686. doi:10.1145/3828.3835. ISSN 0004-5411. http://www.cs.cmu.edu/~sleator/papers/self-adjusting.pdf.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein (2001). "26. Maximum Flow". Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill. pp. 643–668. ISBN 0-262-03293-7.
- Eugene Lawler (2001). "4. Network Flows". Combinatorial Optimization: Networks and Matroids. Dover. pp. 109–177. ISBN 0486414531.
Further reading
- Schrijver, Alexander, "On the history of the transportation and maximum flow problems", Mathematical Programming 91 (2002) 437-445